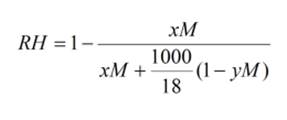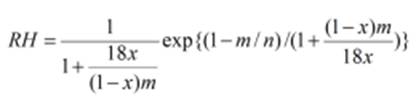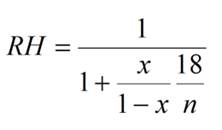Crystal Dehydration

The EMBL HC1 Humidity Control device allows the modulation of the diffraction properties of crystals by controlled dehydration. The first step in a dehydration experiment is to define the relative humidity in equilibrium with the mother liquor of the system under study; this can often be quite time-consuming. In order to reduce the time spent on this stage of the experiment, the equilibrium relative humidity for a range of concentrations of the most commonly used precipitants has been measured. The relationship between the precipitant solution and equilibrium relative humidity is explained by Raoult's law for the equilibrium vapour pressure of water above a solution. The concentration of buffers, additives and detergents used will have a negligible effect on the RH in equilibrium with the mother liquor and is dominated by the primary precipitant.

Use the applet below to predict the RH in equilibrium with your mother liquor before the experiment. Once here the value can be refined using the HC1.

Contact Matthew Bowler for help. Please cite Wheeler, M.J., et al. (2012) Acta Cryst. F68, 111-114 if you use these equations to calculate the RH in equilibrium with solutions or for starting points for experiments using the HC1 humidity control device.

The Relative Humidity (RH) in equilibrium with solutions can be understood in terms of Raoult's law.  It has two aspects that are counter-intuitive and lead to some surprising observations. The first is that the number of equivalent molecules in solution must be accounted for. This means that for sodium chloride, each ion in solution counts as a molecular equivalent. This requires knowledge of the ionization behaviour of the substance in solution. For example, ammonium sulfate effectively dissociates into two ions [NH₄⁺ and (NH₄SO₄)^-] and not three as might be expected.  Raoult's law starts to break down for PEG solutions over a molecular weight of 1000 Da but this can be corrected using the Flory-Huggins model for the entropy of mixing (used in equation 2).

Equation 1: This equation will enable you to calculate the Relative Humidity in equilibrium with a salt solution. You will need to provide the concentration in Mol, the ionisation state of the salt (how many species it dissociates into) and a term describing the the specific volume of the solute (for sodium chloride y = 0.027, for ammonium sulfate y = 0.074, for sodium acetate y = 0.054, for sodium malonate y = 0.095, for magnesium sulphate y = 0.045, for Monopotassium phosphate y = 0.058 and for Dipotassium phosphate y = 0.071). Raoult's law breaks down for lithium chloride (y=0.023) concentrations over 2.5M with RH values much lower than predicted.

Equation 2: where RH is the relative humidity, x is the mass fraction of solute, n is the molecular weight of the polymer and m is a parameter for a polymer such that the ratio n/m is the number of segments of polymer, each of which takes up one space in the disordered lattice. We have found that a value of 38 Da gives a best fit to experimental rather than the actual value of 44 Da for PEGs. Thus, m is approximately the molecular weight of the monomer, when each of the segments is a monomer. For n>>m the dependence on n diminishes as a function of the mass fraction x, so the relative humidity curve has a very nearly universal shape for polymers of molecular mass above ca. 1000 Da. Therefore, the RH equilibrium points for all PEGs of >1000 Da will be equal.

Equation 3: This equation will allow you to calculate the Relative Humidity (RH) in equilibrium with solutions of substances that neither dissociate into multiple species nor are polymers (e.g glycerol, ethylene glycol, sucrose, TMAO, etc)